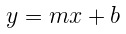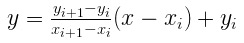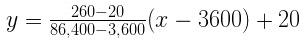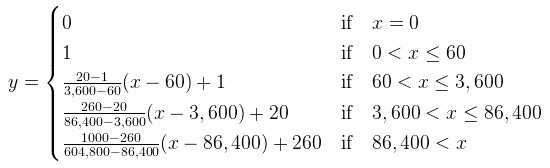Developer Wolfgang Graebner (Wolfgang Graebner) in his blog disassembled Clash of Clans into formulas. We offer a short version of the material in Russian.
Supercell monetize players’ impatience. How? Let’s see what Wolfgang discovered.
The cost of hard currency in the game
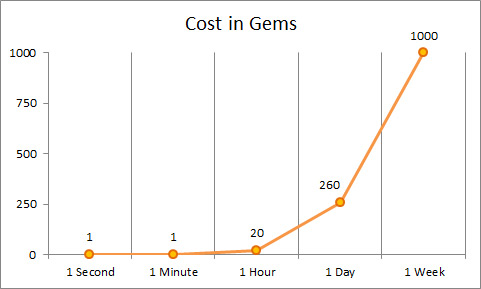
Let’s start with the Cost in Gems chart.
The line on the graph shows how many gems it costs to squander time. More time = more gems.
Attention: the price does not increase exponentially.
The graph resembles an exponent only for the reason that the difference between 60 seconds (1 minute) and 604800 seconds (1 week) is huge. Time grows exponentially, but not the cost.
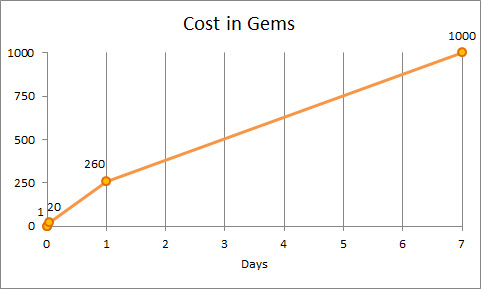
This can be seen on the graph with equal time intervals (in 1 day): the abscissa axis grows evenly.
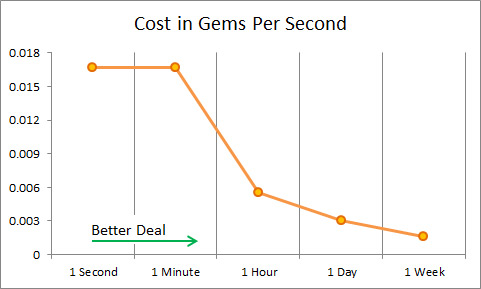
But if we build a graph where the measure is 1 second, not 1 day (Cost in Gems Per Second), then we will see that the price is not rising, it will fall. In other words, the more time you want to skip, the more profitable the deal is for you.
It is clear that this graph is constructed from linear segments. It’s not a curve. According to Wolfgang, this is important.
Key Formulas of Clash of Clans
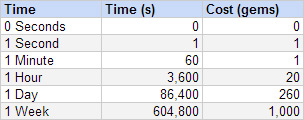
The construction of such a graph (linearly segmented) takes place using the following table, in which it is necessary to set the time periods of interest and their cost in game hard currency.
Wolfgang cites the following as the main advantage of using this particular table:
Dividing by seconds/hours/days/weeks makes it easy to visualize everything. Everyone can easily figure out what is 1 minute for him and what is 1 day. In addition, it is very easy to configure. If you decide that 1 day should cost more, you will need to change only one value.
In other words, the main advantage of using a linear segmented chart is that it allows you to assign and adjust specific price values.
How to build similar graphs and tables?
Of course, using formulas.
To construct a linear equation , this:
From here we can calculate the equation of the line between two points (xi , yi) and (xi+1 , yi+1)
- x – horizontal axis (time);
- y is the vertical axis (gems).
Then you can already experiment.
Using Clash of Clans data, let’s imagine that you want 1 hour (3600 seconds) to cost 20 gems, and 1 day (86400 seconds) to cost 260 gems.Based on this, we stand the following function:
We can use this function to find the cost of any time between 1 hour and 1 day. For example, to find the cost of rewinding 4 hours, substitute x as equal to 14400 seconds and get 51 gems.
All formulas for constructing a linear function can be embedded in a piecewise given function.
Money
After talking about the pricing of time, Wolfgang suggests calculating the real price of time in the game. To do this, he starts by bringing the prices of hard currency in the game and searching for the average price of one gemstone in it.
To determine the cost of one day, he used the formula a little higher and found out that someone at Supercell decided that it would cost, on average, £1.43 to skip one day in Clash of Clans, and a week – £5.49.
The feature, as far as we understood, is that when changing any variable, everyone will also pull up to the desired value.
Sales
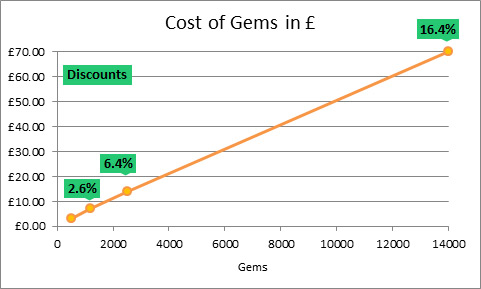
Packs of gems in Clash of Clans are fixed. You can’t buy 501 gems. You can either purchase a pack of 500 gems, or a pack of 1200 gems. On the Cost Gems in £ chart it looks like this:
Supercell gives you a discount if you buy a lot.
You save about 16.4% by buying a pack of 14,000 gems, compared to buying 500 gems.
Scrolling through the time
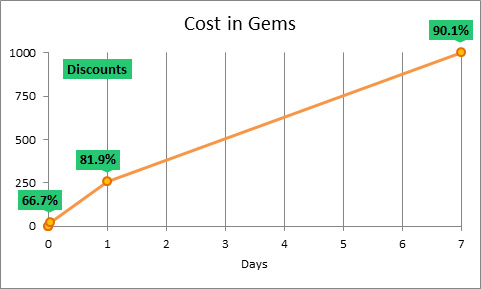
When comparing gemstone discounts and time-scrolling discounts, it becomes obvious that time-skipping discounts are much more generous.
You save about 90.1% by buying a skip of one week, compared to if you wanted to skip 1 minute.
It is worth noting that the difference in discounts between 1 minute and 1 hour is 66.7%, but the difference in discounts between 1 hour and 1 week is only 23.4%. Instead of thinking about high discounts for 1+ day, I suggest thinking about the reasons for the high cost of 1-59 minutes. Why are they so expensive? I don’t have a clear ovtet. I suspect that only the most impatient players will want to pay for such short-term skips.
Compare discounts
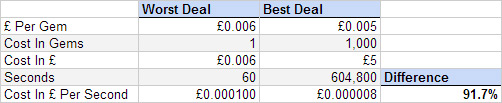
If you buy gems and then use them to scroll through time, they overlap each other.
The worst deal is if you buy 500 gems for £2.99 and then spend them on a skip of 1 minute. You pay £0.000100 for the second you skip.
The best deal: Buying 14,000 crystals for £69.99 and using it to scroll for 1 week. Then you only pay £0.000008 per second.
The difference in price is 91.7%
The power of discount
The cost of each second does not sound very serious in both cases, but when you skip 640800 seconds, they add up and turn into serious figures. For example, if you missed 1 week at the price that you miss 1 minute, it would cost you not 5 pounds, but all 60.
Generous discounts on skipping time – play a very important role. Without them, prices would quickly become prohibitively high and no one would spend money on skipping time.
Total
- The longer the period of time you miss, the larger the required amount, but, in general, a better deal.
- The graph of the price algorithm is constructed from linear segments.
- The beauty of a graph constructed from linear segments is that it allows you to assign and adjust specific prices accurately and clearly.
- The discount for skipping a long period of time is more important than the discount for buying more crystals.
- A generous discount on skipping a long period of time is not necessary. Without it, prices will quickly become high for users.
The full version of the original article can be found here.
Wolfgang’s blog is here.
All graphs, tables and formulas are taken from the original material.
A source: http://www.gamasutra.com/