How to simulate viral growth: a hybrid model

How to simulate viral growth: a hybrid model

What is a viral product?

Users come to the product in various ways: through the press, advertising, your advertising partner campaigns. But one of the most interesting channels is the users themselves. 

A key factor in the growth of a viral product is the recruitment of new users by existing users. The user can simply invite another person (“Look at this product, it’s cool/useful/interesting”) or directly using the product (“I want to send you money via PayPal”).

One of the most famous viral examples is YouTube. Before the site became a huge collection of videos, you could most likely find its videos embedded in news sites and personal blogs. You viewed them, and at the end you were asked to send a link to them to people you know, and also given a code to embed the video into your site. If you didn’t want to share it, then YouTube offered a set of other videos that you might like and that you could share. Your friends watched the videos you shared, sent it to their friends, and so on in a circle – a “viral cycle” arose, in which YouTube acquired users at an unprecedented speed.

How can we predict how the virality of our product will work? How long will it take him to recruit 1 million users? Will he get 10 million? And 100 million?

To answer these questions, we need to build a virality model.

In this example, we will conduct experiments with the Excel spreadsheet “How to model viral growth.xlsx».

The simplest model

Let’s say we started with 5,000 users. What kind of organic is worth waiting for? 

Well, some will like our product, and some will not. Some will invite a lot of people, and some no one. Some will be invited in a day, and some will need a week.

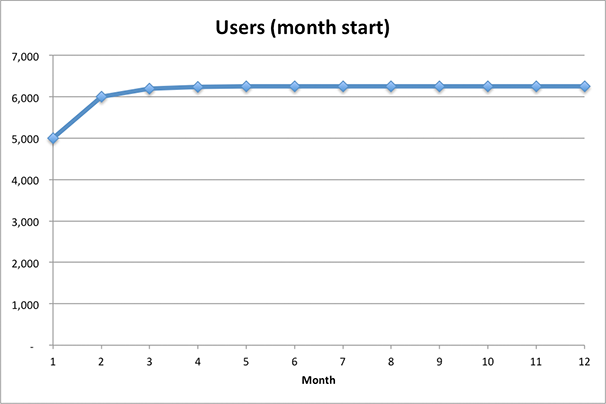
Let’s put aside all these uncertainties and say that, on average, 1 out of 5 of our users in the first month will attract 1 new user. In other words, our virality factor is 1/5 = 0.2 and our 5,000 initial users will gain 5,000 * 0.2 = 1,000 users per Month 1. This 1,000 will then gain another 1,000 * 0.2 = 200 in Month 2, which will then recruit another 200 * 0.2 = 40 in Month 3 and so on.

What our growth will look like (see the table on Sheet 1):

We will acquire users at a decreasing rate up to 6,250 people.

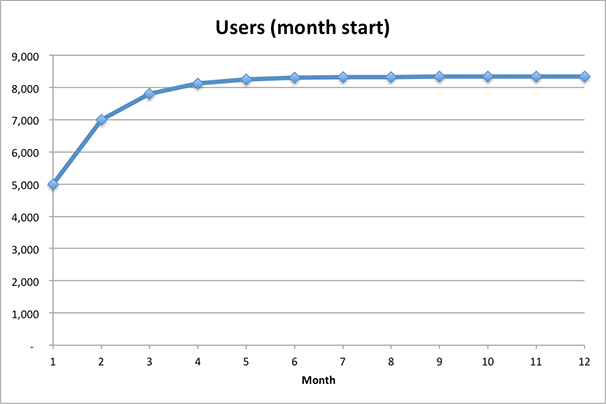
What will happen if our virality factor is increased to 0.4?

As before, we are acquiring users at a decreasing rate, but now our growth rests on 8,300 users.

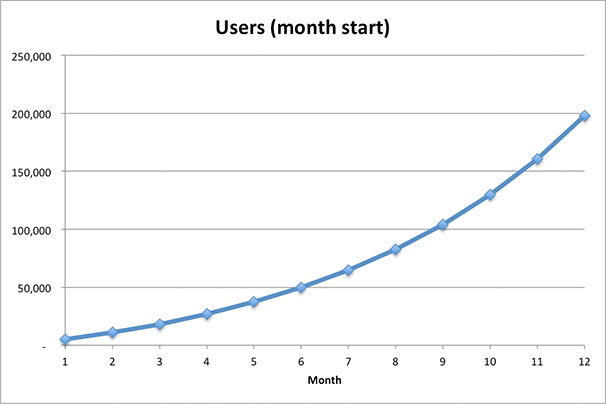
What happens if we set the virality factor to 1.2?

This time we are acquiring users at an increasing rate!

In fact, with the help of simple calculations, you can show the following:

• with x initial users and a viral factor v less than 1, we will acquire users at a decreasing rate up to x/(1-v) users;
• with a viral factor greater than 1, the number of our users will grow all the time.

Everything is simple. All we have to do is get a virality factor greater than 1, right?

Well, not right…

Firstly, a lot of things are not taken into account in our model. For example, as we acquire new users, we will run out of new ones who can still be invited. I won’t go into much detail about this here, but to learn more about this effect, read “Facebook Viral Marketing: When and Why do Apps Start Going Downhill?” Andrew Chen.

Secondly, viral growth is incredibly rare. It took me some time to evaluate: very few products have a sustained virality factor greater than 1 for any sane period of time. But if we cannot rely on the fact that the virality factor will be greater than 1, what should we use in our model?

From discussions with other entrepreneurs, investors and “growth hackers”, I realized the following: for consumer Internet products, a stable virality factor from 0.15 to 0.25 is good, 0.4 is great, and about 0.7 is simply outstanding.

However, we have already shown that with a virality factor of less than 1, we acquire users at a decreasing rate until the growth ends. It’s not what everyone wants, so what’s missing from the picture?

We missed out on all the other channels that can bring users: press, app stores, direct traffic, inbound marketing, paid advertising, partnerships, cross-promos, search engine marketing, SEO, celebrity support and everything else we can think of. Let’s revise our model and take into account the influence of these factors.

Hybrid model

We will rebuild our model to account for non-viral channels (Sheet 2 in the table).

Some non-viral channels – such as the press – will give us a quick surge of users, while others — such as app stores – will give us a steady stream of users. Let’s take both types into account in our model and, for simplicity, we will count only three non-viral channels:

• The press: a good start can attract up to 70,000 people.
• Search traffic in app stores. Up to 40,000 downloads per month. Not all users will launch our application, and of those who will launch, not all will register or be satisfied with their first experience in it. Let’s assume that 60% will like the app.
• Direct traffic. Since our users and potential users tend to talk, people will find our product directly. This can attract up to 10,000 downloads per month. Again, let’s assume that only 60% of them will remain.

Finally, let’s assume for simplicity that traffic from the store and direct traffic will remain constant over time.

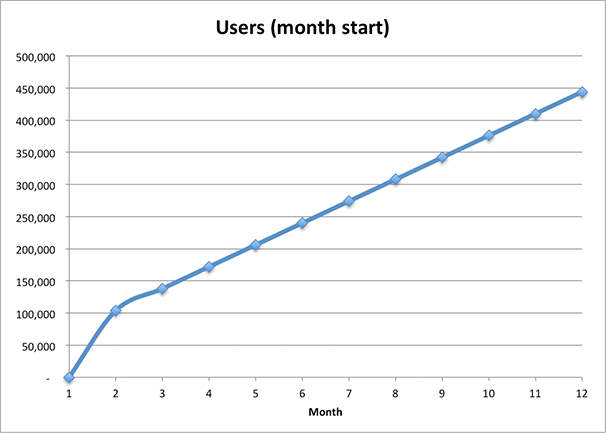
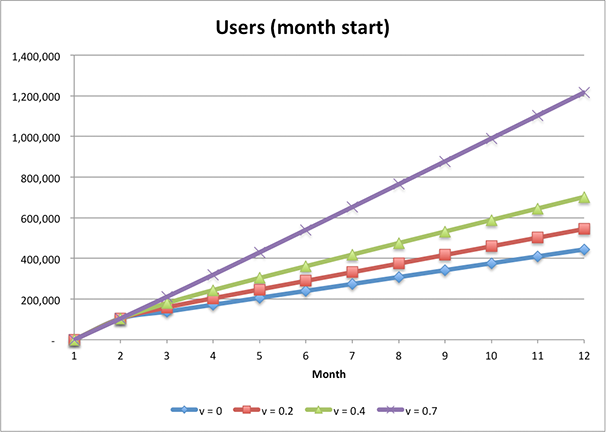
Let’s set our virality factor to 0 and see how our product will live without a viral component at all.

By the end of the year we will have 450,000 users. Let’s test different cases of virality.

In a good case, with a virality factor of 0.2., by the end of the year we will have 500,000 people. With an excellent development of events, with a factor of 0.4, by the end of the year we will have 700,000 users. And in the most excellent, with a factor of 0.7, at the end of the year we will have 1.2 million loyal fans.

Gain factor

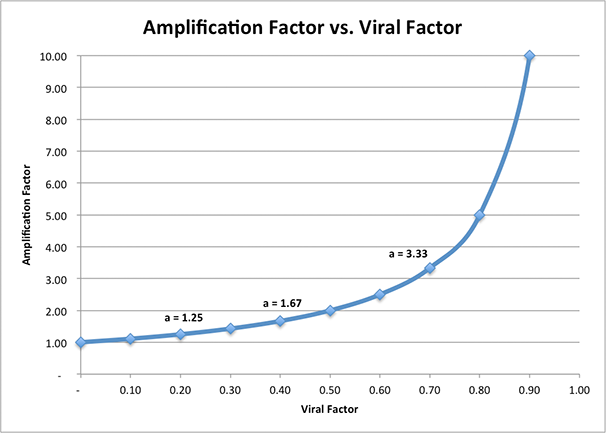
This model shows how I often think of virality: not as a virality factor v, but as a gain factor a = 1/(1-v). To calculate our total number of users, we just need to multiply the number of users acquired through non-viral channels by the gain factor.

This graph shows the amazing potential of the viral factor, even if it is less than 1: by increasing our viral factor, we increase the gain hyperbolically (advice for professionals: to troll other startups, try to tell them that your growth is hyperbolic).

With the help of virality factors, we can, several times, increase our acquisition of users through non-viral channels. But remember: you can’t amplify something that doesn’t exist! That’s why we have to divide our growth efforts between non- and viral channels. If we only do one thing, we’ll lose everyone.

Our users are immortal

Adding non-viral channels helps, but there is still a significant flaw in our model. For example, we assume that incoming users stay in the application forever.

This is extremely optimistic: we refuse certain products all the time. We can forget about him. We may stop liking him. Perhaps we never liked him. In my next article, we will make changes to my model, taking into account the loss of users.

You can read it here.

Resume

• Viral growth is very rare: for a consumer Internet product, a stable viral factor from 0.15 to 0.25 is good, 0.4 is great, and 0.7 is outstanding.
• When the virality factor is less than one, it can be considered as a gain factor a = 1/(1-v). To calculate the total number of users, multiply the number of people from non-viral channels by the gain factor.
• When the virality factor is less than one, it is critically important to have strong stable non-viral channels.
• A small increase in the viral factor can cause a large increase in the gain.

The article was published as part of a joint series of materials “The Freemium Code” of mobile development sites App2Top.ru and Apptractor.ru .

Original material: https://www.linkedin.com/today/post/article/20121002124206-18876785-how-to-model-viral-growth-the-hybrid-model

Original translation: http://apptractor.ru/info/articles/virusnyj-rost-model.html